こんにちは。12月30日のブログ担当の雲井です。
どれだけの人が楽しめるか分かりませんが、数学の図形の話です。
中学3年生の数学では、図形の相似(そうじ)を学習しましたね。この相似という考え方は、実は私たちの身の回りの色々なところにつながっています。
冬休みに入る前に、この相似をさらに深掘りして、ちょっと不思議な形「トーラス」の世界をのぞいてみましょう!
1.相似の前に「合同」を振り返ろう
まず、中学2年生の証明で学んだ合同(ごうどう)を思い出してください。
(※「合同」という語句自体は小学校5年生で学んでいるはずです…)
合同とは?
2つの図形がぴったり重なること。
形も大きさも全く同じ、つまり「完璧なコピー」です。
対応する辺の長さはすべて等しく、対応する角の大きさもすべて等しい。
どれだけの人が楽しめるか分かりませんが、数学の図形の話です。
中学3年生の数学では、図形の相似(そうじ)を学習しましたね。この相似という考え方は、実は私たちの身の回りの色々なところにつながっています。
冬休みに入る前に、この相似をさらに深掘りして、ちょっと不思議な形「トーラス」の世界をのぞいてみましょう!
1.相似の前に「合同」を振り返ろう
まず、中学2年生の証明で学んだ合同(ごうどう)を思い出してください。
(※「合同」という語句自体は小学校5年生で学んでいるはずです…)
合同とは?
2つの図形がぴったり重なること。
形も大きさも全く同じ、つまり「完璧なコピー」です。
対応する辺の長さはすべて等しく、対応する角の大きさもすべて等しい。
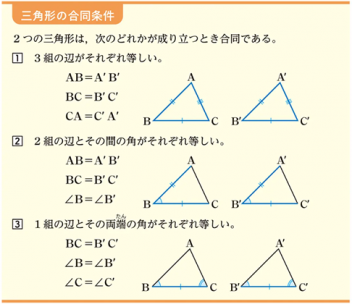
※ 出典『中学数学2』(教育出版)
2.形は同じ、大きさは違ってもOK!「相似」の世界
次に、皆さんが今学んだ相似(そうじ)です。
(※「相似」の概念は小学校6年生の「拡大図、縮図」学んでいるはずです…)
相似とは?
片方の図形を、形を変えずに拡大(大きく)または縮小(小さく)したときに、もう一方の図形にぴったり重ねられること。
言ってみれば「拡大・縮小されたコピー」です。
対応する角の大きさはすべて等しい。
対応する辺の長さの比(相似比)がすべて等しい。
2.形は同じ、大きさは違ってもOK!「相似」の世界
次に、皆さんが今学んだ相似(そうじ)です。
(※「相似」の概念は小学校6年生の「拡大図、縮図」学んでいるはずです…)
相似とは?
片方の図形を、形を変えずに拡大(大きく)または縮小(小さく)したときに、もう一方の図形にぴったり重ねられること。
言ってみれば「拡大・縮小されたコピー」です。
対応する角の大きさはすべて等しい。
対応する辺の長さの比(相似比)がすべて等しい。
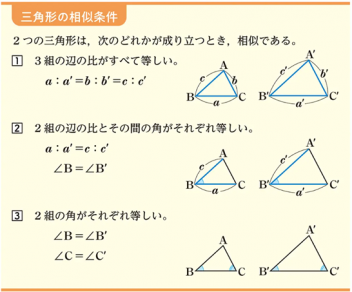
※出典『中学数学3』(教育出版)
相似は、私たちが遠くの山や建物の高さを測ったり、地図を作ったり、模型を作ったりするときに欠かせない考え方です。
合同は「相似比が 1:1 の相似」と考えることもできますね!
3.相似の先にある不思議な図形「トーラス」
さて、ここからが今回のハイライトです!相似という概念が「形はそのままに、大きさを変える」というものだとすれば、さらに「大きさも形も柔軟に変えられる」数学の世界があります。それが「位相幾何学(いそうきかがく)」という分野です。
そして、その位相幾何学でとても有名で面白い図形が「トーラス(Torus)」です。
トーラスとは?
簡単に言えば、ドーナツや浮き輪のような、真ん中に穴が開いた立体(曲面)のことです。
トーラスの面白い性質
トーラスの面白さは、その「穴の数」にあります。
位相幾何学では、図形をゴムのように自由に引き延ばしたり、曲げたり、ねじったりしても、破ったり、くっつけたりしない限り、その図形が持つ本質的な性質は変わらないと考えます。
例えば、
球体(ボール)には、穴は0個。
トーラス(ドーナツ)には、穴は1個。
球体は、変形してもコップやお茶碗など、穴のない形にしかなりません。
トーラスは、変形してもマグカップのように持ち手という穴が1つある形にしかなりません。(これを「マグカップとドーナツは同じ形」という面白い表現で説明することもあります!)※“合同”や“相似”、のような言い方にすると、
マグカップとドーナツは“位相同型(同相)”という言い方をします。
相似は、私たちが遠くの山や建物の高さを測ったり、地図を作ったり、模型を作ったりするときに欠かせない考え方です。
合同は「相似比が 1:1 の相似」と考えることもできますね!
3.相似の先にある不思議な図形「トーラス」
さて、ここからが今回のハイライトです!相似という概念が「形はそのままに、大きさを変える」というものだとすれば、さらに「大きさも形も柔軟に変えられる」数学の世界があります。それが「位相幾何学(いそうきかがく)」という分野です。
そして、その位相幾何学でとても有名で面白い図形が「トーラス(Torus)」です。
トーラスとは?
簡単に言えば、ドーナツや浮き輪のような、真ん中に穴が開いた立体(曲面)のことです。
トーラスの面白い性質
トーラスの面白さは、その「穴の数」にあります。
位相幾何学では、図形をゴムのように自由に引き延ばしたり、曲げたり、ねじったりしても、破ったり、くっつけたりしない限り、その図形が持つ本質的な性質は変わらないと考えます。
例えば、
球体(ボール)には、穴は0個。
トーラス(ドーナツ)には、穴は1個。
球体は、変形してもコップやお茶碗など、穴のない形にしかなりません。
トーラスは、変形してもマグカップのように持ち手という穴が1つある形にしかなりません。(これを「マグカップとドーナツは同じ形」という面白い表現で説明することもあります!)※“合同”や“相似”、のような言い方にすると、
マグカップとドーナツは“位相同型(同相)”という言い方をします。

※ Geminiで作成した画像です
穴の数が違う図形同士は、どんなに頑張って変形しても同じ形にはなれない、ということが数学的に証明されています。
4.冬休みは身の回りの相似やトーラスを探そう!
合同から始まり、拡大・縮小の相似、そして穴の数に着目するトーラスへと、数学の世界はどんどん深くて面白くなっていきます。
冬休みは、ぜひ身の回りにある色々なものに目を向けてみてください。
小さな模型と本物の建物との相似比はいくつだろう?
お母さんが作るドーナツの形は、数学で言うトーラスそのものだな!
穴の開いたものは、他にどんな形があるかな?(もし穴が2つあったら、それは「ダブルトーラス」という別の図形になります!)※トーラスで調べて、分かりやすい動画を探してみるのも良いかもしれません…
皆さんが数学で学んだことが、世界を見る新しい「目」になります。冬休みも、この知的好奇心と探究心を大切にして、楽しく過ごしてくださいね!
3学期に、また元気な皆さんに会えるのを楽しみにしています!良いお年を!
穴の数が違う図形同士は、どんなに頑張って変形しても同じ形にはなれない、ということが数学的に証明されています。
4.冬休みは身の回りの相似やトーラスを探そう!
合同から始まり、拡大・縮小の相似、そして穴の数に着目するトーラスへと、数学の世界はどんどん深くて面白くなっていきます。
冬休みは、ぜひ身の回りにある色々なものに目を向けてみてください。
小さな模型と本物の建物との相似比はいくつだろう?
お母さんが作るドーナツの形は、数学で言うトーラスそのものだな!
穴の開いたものは、他にどんな形があるかな?(もし穴が2つあったら、それは「ダブルトーラス」という別の図形になります!)※トーラスで調べて、分かりやすい動画を探してみるのも良いかもしれません…
皆さんが数学で学んだことが、世界を見る新しい「目」になります。冬休みも、この知的好奇心と探究心を大切にして、楽しく過ごしてくださいね!
3学期に、また元気な皆さんに会えるのを楽しみにしています!良いお年を!