頭を使い始めましょう！

2013年1月3日

中３数学では、円を学習しました。以下の４つ（①②③は定理）について学習しました。

①「円周角の定理」(1)1つの弧に対する円周角の大きさは、その弧に対する中心角の大きさの半分である。
(2)同じ弧に対する円周角の大きさはすべて等しい。

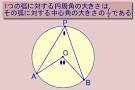
②１つの円で、(1)等しい弧に対する円周角は等しい。(2)等しい円周角に対する弧は等しい。

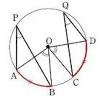
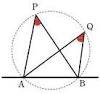
③2点Ｐ，Ｑが直線ＡＢについて同じ側にあるとき、∠ＡＰＢ＝∠ＡＱＢならば、４点Ａ，Ｂ，Ｐ，Ｑは１つの円周上にある。

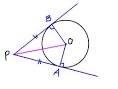
④円外の１点からその円にひいた２つの接線の長さは等しい。

では、円に絡めて次のことを試してみてください。
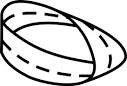
（１）　１本のテープを１回ひねってから、両端をつないで輪にする。
（２）　次に、その輪の幅半分（下図の点線）の所を切っていく。
（３）　広げると・・・どうなるでしょう？

ぜひ、実践してみてください。　
これは、ドイツの数学者メビウス（１７９０～１８６８）が、考え出したものでメビウスの輪と呼ばれ、表と裏がない曲面をもつ不思議なものになります。